Gammatone 滤波器
Gammatone滤波器冲击响应(Impulse response, IR):
\[\begin{equation} \begin{aligned} g(t) = \frac{at^{n-1}\cos(2\pi f_ct+\phi_0)}{e^{2\pi b t}} \end{aligned} \end{equation}\]其中 \(\begin{equation} \begin{aligned} \begin{cases} n: 阶数,一般为4;\\ f_c:中心频率;\\ b:3dB 带宽;\\ \phi_0:初始相位 \end{cases} \end{aligned} \end{equation}\)
滤波器的频谱
\(g(t)\) 可分解为两部分的乘积,即
\[\begin{equation} \begin{aligned} g(t)=a \times r(t) \times s(t) \end{aligned} \end{equation}\]其中
\[\begin{equation} \begin{aligned} r(t)&=t^{n-1}e^{-2\pi bt}\\ s(t)&=cos(2\pi f_c t+\phi_0) \end{aligned} \end{equation}\]时域相乘==频域卷积,即:
\[\begin{equation} \begin{aligned} G(f)=a\times R(f)*S(f) \end{aligned} \end{equation}\]-
计算\(R(f)\)
\[\begin{equation} \begin{aligned} R(f)=FT(t^{n-1}e^{-2\pi b t}) &=\frac{1}{(j2\pi)^{n-1}}\frac{\partial^{n-1} FT(e^{-2\pi bt})}{\partial f^{n-1}}\\ &=\frac{(n-1)!}{(2\pi b)^n}\frac{1}{(1+jf/b)^n}\\ \end{aligned} \end{equation}\]令 \(c=\frac{(n-1)!}{(2\pi b)^n}\),上式可写作
\[\begin{equation} \begin{aligned} R(f) = c\frac{1}{(1+jf/b)^n} \end{aligned} \end{equation}\] -
计算\(S(f)\)
\[\begin{equation} \begin{aligned} S(f)&=FT\left(cos(2\pi f_ct+\phi_0)\right)\\ &=e^{j\phi_0}\delta(f-f_c)+e^{-j\phi_0}\delta(f+f_c) \end{aligned} \end{equation}\]
综上,有
\[\begin{equation} \begin{aligned} G(f)&=a \times R(f)*S(f)\\ &=a \times e^{j\phi_0}c\frac{1}{(1+j(f-f_c)/b)^n}+ae^{-j\phi_0}c\frac{1}{(1+j(f+f_c)/b)^n}\\ &=ac\left[e^{j\phi_0}\left(\frac{1}{(1+j(f-f_c)/b)}\right)^n+e^{-j\phi_0}\left(\frac{1}{(1+j(f+f_c)/b)}\right)^n\right] \end{aligned} \end{equation}\]滤波器幅频曲线示意图如下
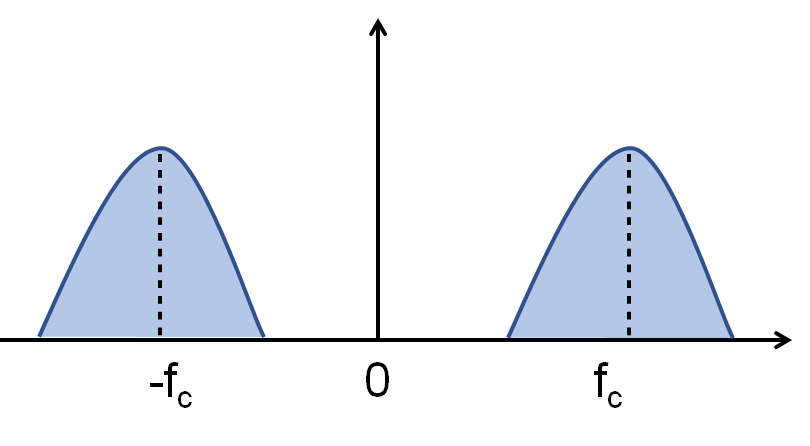
3dB带宽 & ERB
听觉滤波器的带宽通常用等效矩形带宽(Equalization rectangular bandwidth, ERB)1表示。
Gammatone 滤波器的ERB可计算得到(计算过程见附录))
\[\begin{equation} \begin{aligned} ERB(f_c) = \frac{\int_{f=0}^{\infty}{|g(f)|^2df}}{g(f_c)}\approx\frac{15\pi}{48}b \end{aligned} \end{equation}\]可以得到3dB带宽和ERB之间的关系
\[\begin{equation} \begin{aligned} b \approx \frac{48}{15\pi}ERB(f_c) \approx 1.019 ERB(f_c) \end{aligned} \end{equation}\]增益和相移
以 \(cf=4 kHz\) 的滤波器为例,\(G(f)\) 对应的幅频、相频响应曲线如下
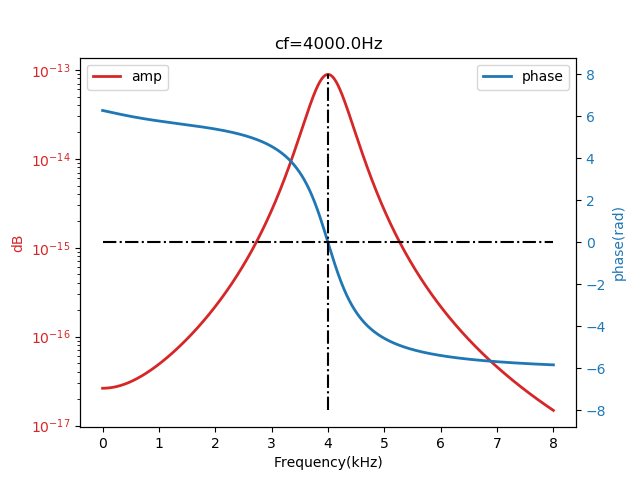
在中心频率处,即 \(f=f_c\),Gammatone滤波器的增益 \(G(f_c)\) 可计算得到
\[\begin{equation} \begin{aligned} G(f_c)&=\left.ac\left[e^{j\phi_0}\left(\frac{1}{(1+j(f-f_c)/b)}\right)^n+e^{-j\phi_0}\left(\frac{1}{(1+j(f+f_c)/b)}\right)^n\right]\right|_{f=f_c}\\ &=ac\left[e^{j\phi_0}+e^{-j\phi_0}\frac{1}{(1+2jf_c/b)^n}\right]\\ &=ac\left[e^{j\phi_0}+e^{-j\phi_0}\frac{1}{(1+2jQ)^n}\right] \end{aligned} \end{equation}\]其中,\(Q=\frac{f_c}{b}\),即滤波器的品质因数。
当 \(\begin{equation}\begin{aligned} \begin{cases} \phi_0=0\\ n = 4 \end{cases} \end{aligned}\end{equation}\),滤波器在中心频率处的响应 \(G(f_c)\)
\[\begin{equation} \begin{aligned} G(f=f_c)&=\frac{(n-1)!}{(2\pi b)^n }\left[1+\frac{1}{(1+j2Q)^n}\right]\\ &=\frac{6}{(2\pi b)^4}\left[\frac{16Q^4-24Q^2+2+8jQ(1-4Q^2)}{16Q^4-24Q^2+1+8jQ(1-4Q^2)}\right]\\ &=\frac{3}{(2\pi b)^4}\frac{r_1e^{\phi_1}}{r_2e^{\phi_2}}\\ \end{aligned} \end{equation}\]其中 \(\begin{equation} \begin{aligned} \begin{cases} r_1 = \sqrt{(16Q^4-24Q^2+2)^2+(8Q-32Q^3)^2}\\ \phi_1 = \arctan{\frac{8Q-32Q^3}{16Q^4-24Q^2+2}}\\ r_2 = \sqrt{(16Q^4-24Q^2+1)^2+(8Q-32Q^3)^2}\\ \phi_2 = \arctan{\frac{8Q-32Q^3}{16Q^4-24Q^2+1}} \end{cases} \end{aligned} \end{equation}\)
对应的增益和相移分别为
\[\begin{equation} \begin{aligned} Gain_{f_c} &= \frac{3}{(2\pi b)^4}\frac{\sqrt{(16Q^4-24Q^2+2)^2+(8Q-32Q^3)^2}}{\sqrt{(16Q^4-24Q^2+1)^2+(8Q-32Q^3)^2}}\\ \phi_{f_c} &= \arctan{\frac{8Q-32Q^3}{16Q^4-24Q^2+2}}-\arctan{\frac{8Q-32Q^3}{16Q^4-24Q^2+1}}\\ \end{aligned} \end{equation}\]不同中心频率处的增益和相移如下
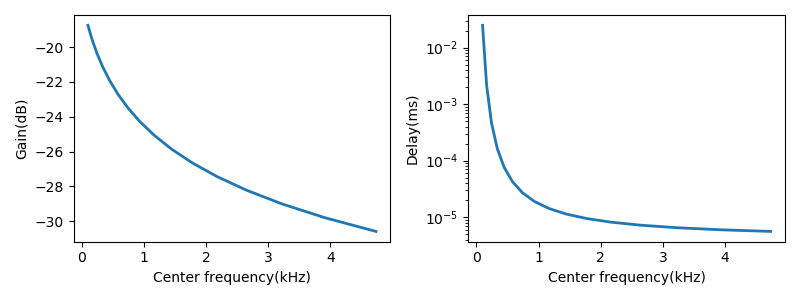
根据Glassberg & Moore2 给出的ERB的公式
\[\begin{equation} \begin{aligned} ERB(f_c)=24.7*4.37/1000*f_c+24.7 \end{aligned} \end{equation}\]有
\[\begin{equation} \begin{aligned} Q=\frac{f_c}{b}=\frac{f_c}{1.019ERB(f_c)}=\frac{1}{0.110+25.2/f_c} \end{aligned} \end{equation}\]随着中心频率的增大,Q越来越大,此时增益中 \(\frac{1}{(1+2jQ)^n}\) 可以近似忽略,此时中心频率处:
\[\begin{equation} \begin{aligned} \begin{cases} G(f_c)=\frac{a(n-1)!}{(2\pi b)^n}\\ \phi(f_c) = 0 \end{cases} \end{aligned} \end{equation}\]数字滤波器设计–Base-band 冲击响应不变3
如前所述,\(G(f)\) 可以看作由 \(R(f)\) 和 \(S(f)\) 卷积得到:
- \(R(f)\) 是低通滤波器,由n个一阶低通滤波器及联得到;
- \(S(f)\) 的功能则是频率搬移,将低通滤波器转换为带通滤波器。
在设计滤波器的时候,可以反过来,首先对输入信号降频 \(f_c\) ,然后在应用低通滤波器 \(R(f)\) ,问题就变的简单了。
-
\[\begin{equation}
\begin{aligned}
x'(t)=e^{j2\pi f_c t}x(t)
\end{aligned}
\end{equation}\]
这里其实只考虑了单边谱,因此计算增益的时候应该 \(\times 2\)
-
低通滤波器的设计
使用冲击响应不变法,对 \(r(t)\) 进行采样,采样间隔为T,即:
\[\begin{equation} \begin{aligned} r_d(i) = r(iT)= (iT)^{n-1}e^{-2\pi bTi}=T^{n-1}i^{n-1}e^{-2\pi bTi}\label{eq1} \end{aligned} \end{equation}\]令 \(k=e^{-2\pi bT}\) ,上式就可以简化为
\[\begin{equation} \begin{aligned} r_d(i)=T^{n-1}i^{n-1}k^{i} \end{aligned} \end{equation}\]因为
\[\begin{equation} \begin{aligned} Z(if(i))=\sum{if(i)z^{-i}} &=-z\frac{\partial\sum{f(i)z^{-i}}}{\partial z}\\ &=z^{-1}\frac{\partial Z(f(i))}{\partial z^{-1}}\\ Z(k^{i})=\frac{1}{1-kz^{-1}} \end{aligned} \end{equation}\]所以
\[\begin{equation} \begin{aligned} Z(ik^i)&=z^{-1}\frac{\partial Z(k^{i})}{\partial z^{-1}}=z^{-1}\frac{\partial \frac{1}{1-kz^{-1}}}{\partial z^{-1}}=\frac{kz^{-1}}{(1-kz^{-1})^2}\\ Z(i^2k^i)&=z^{-1}\frac{\partial Z(iz^{i})}{\partial z^{-1}}=z^{-1}\frac{\frac{kz^{-1}}{(1-kz^{-1})^2}}{\partial z^{-1}}=z^{-1}\left[\frac{k}{(1-kz^{-1})^2}+\frac{2k^2z^{-1}}{(1-kz^{-1})^3}\right]\\ Z(i^3k^i)&=z^{-1}\frac{\partial Z(i^2k^{i})}{\partial z^{-1}}=z^{-1}\frac{z^{-1}\left[\frac{k}{(1-kz^{-1})^2}+\frac{2k^2z^{-1}}{(1-kz^{-1})^3}\right]}{\partial z^{-1}}\\ &=\frac{kz^{-1}(1+4kz^{-1}+k^2z^{-2})}{1-4kz^{-1}+6k^2z^{-2}-4k^3z^{-3}+k^4z^{-4}}\\ \end{aligned} \end{equation}\]因此
\[\begin{equation} \begin{aligned} Z\left(r_d(i)\right) &= Z\left(cT^3*i^3k^i\right)=\frac{6T^3}{(2\pi b)^4}Z(i^3k^i)\\ &=T^3\frac{z^{-1}(1+4kz^{-1}+k^2z^{-2})}{1-4kz^{-1}+6k^2z^{-2}-4k^3z^{-3}+k^4z^{-4}}\\ \end{aligned} \end{equation}\]最终得到Gammatone滤波器的公式
\[\begin{equation} \begin{aligned} y'(n)=&T^3\left[\underbrace{x'(n-1)+4kx'(n-2)+k^2x'(n-3)}_\text{分子}\right.+\\ &\left.\underbrace{4ky'(n-1)-6k^2y'(n-2)+4k^3y'(n-3)-k^4y'(n-4)}_\text{分母}\right] \end{aligned} \end{equation}\] -
滤波结果升频
升频后信号的实部即为最终结果,即
\[\begin{equation} \begin{aligned} y(t)=Real(e^{-2\pi fct}y) \end{aligned} \end{equation}\]
中心频率增益归一
因为实现过程中将带通滤波器转换为低通滤波器,因此只需要对低通滤波器0频处的增益归一为1/2即可。 因此,归一化系数应该是
\[\begin{equation} \begin{aligned} scale &= \frac{1}{Z(r_d(i)|_{z=1})/2}\\ &=\frac{1}{T^3\frac{z^{-1}(1+4kz^{-1}+k^2z^{-2})}{1-4kz^{-1}+6k^2z^{-2}-4k^3z^{-3}+k^4z^{-4}}|_{z=1}/2}\\ &= \frac{(1-k)^4}{T^3(1+4k+k^2)} \end{aligned} \end{equation}\]e.g.
| 归一前 | 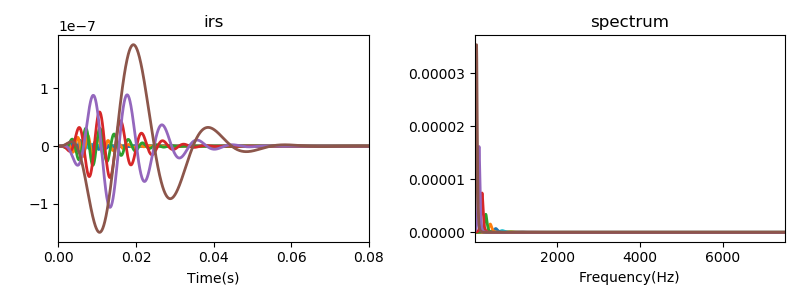 |
| 归一后 | 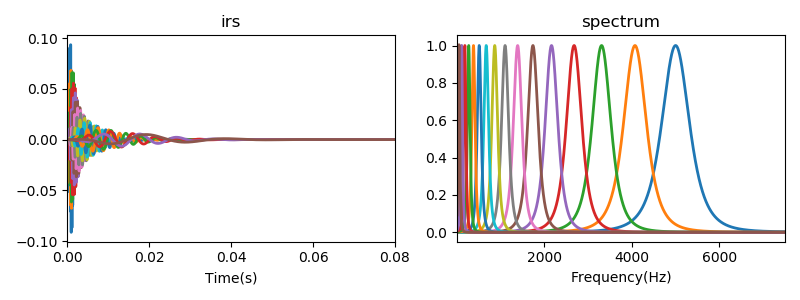 |
误差
低通滤波器经移频之后,左右两部分可能存在overlap,从而使得带通滤波器中心频率处的增益略大于低通滤波器0频处的增益。误差系数为
\[\begin{equation} \begin{aligned} \frac{\sqrt{(16Q^4-24Q^2+2)^2+(8Q-32Q^3)^2}}{\sqrt{(16Q^4-24Q^2+1)^2+(8Q-32Q^3)^2}} \approx 1 \end{aligned} \end{equation}\]附录
频率搬移
对于输入信号x(i),将频率向左移动 \(f_c\) 得到 \(x'(t)\),即:
\[\begin{equation} \begin{aligned} x'(t)=\int_{f}{X'(f)e^{2\pi ft}df} &=\int_{f}{X(f+f_c)e^{2\pi ft}df}\\ &=\int_{f}{X(f+f_c)e^{2\pi (f+f_c)t}e^{-2\pi f_c t}df}\\ &=x(t)e^{-2\pi f_c t} \end{aligned} \end{equation}\]ERB与3dB带宽的转换
如 滤波器频谱示意图 所示,由于双边谱的对称性,计算滤波器输出功率时可以只考虑 \(f>0\) 一侧,即。
\[\begin{equation} \begin{aligned} P=\int_{f=0}^{\infty}{|g(f)|^2df} &\approx \int{\left|ac\left[e^{j\phi_0}\left(\frac{1}{1+j(f-f_c)/b}\right)^n\right]\right|^2df}\\ &= \left(ac\right)^2\int{\left|\left(\frac{1}{r_{f_c}e^{j\phi_{f_c}}}\right)^n\right|^2df}\\ &= \left(ac\right)^2\int{r_{f_c}^{-2n}df} \end{aligned} \end{equation}\]其中 \(r_{f_c}=\sqrt{1+\left(\frac{f-fc}{b}\right)^2}\)
令 \(x=(f-fc)/b, \quad c= \left(ac\right)^2\),有
\[\begin{equation} \begin{aligned} P=c\int{r_{f_c}^{-2n}} &=c\int{(1+x^2)^{-n}bdx}\\ &=bc\int{(1+x^2)^{-n}dx}\\ \end{aligned} \end{equation}\]再令 \(x=tan(y)\),有
\[\begin{equation} \begin{aligned} P=bc\int_{y=0}^{\pi/2}{cos^{2n}(y)d\tan(y)} &=bc\int_{y=0}^{\pi/2}{cos^{2n}(y)cos^{-2}(y)dy}\\ &=bc\int_{y=0}^{\pi/2}{cos^{2n-2}(y)dy} \end{aligned} \end{equation}\]根据分部积分法
\[\begin{equation} \begin{aligned} \int_{x=0}^{\pi/2}{cos^{2n-2}(y)dy} &=\int_{y=0}^{\pi/2}{cos^{2n-3}(y)d\sin(y)}\\ &=cos(y)^{2n-3}sin(y)\left.\right|_{0}^{\pi/2}-\int_{y=0}^{\pi/2}{sin(y)d\cos^{2n-3}(y)}\\ &=\int_{y=0}^{\pi/2}{(2n-3)sin^2(y)cos^{2n-4}(y)dy}\\ &=\int_{y=0}^{\pi/2}{(2n-3)(1-cos^2(y))cos^{2n-4}(y)dy}\\ &=\int_{y=0}^{\pi/2}{(2n-3)cos^{2n-4}(y)}dy-\int_{y=0}^{\pi/2}{(2n-3)cos^{2n-2}(y))dy}\\ \end{aligned} \end{equation}\]移项可得到 \(\int_{x=0}^{\pi/2}{cos^{2n-2}(y)dy}\) 的迭代公式
\[\begin{equation} \begin{aligned} \int_{y=0}^{\pi/2}{(2n-2)cos^{2n-2}(y))dy}&=\int_{y=0}^{\pi/2}{(2n-3)cos^{2n-4}(y)}dy\\ \end{aligned} \end{equation}\]可得到
\[\begin{equation} \begin{aligned} \int_{y=0}^{\pi/2}{cos^{2n-2}(y))dy}&=\int_{y=0}^{\pi/2}{\frac{2n-3}{2n-2}cos^{2n-4}(y)}dy\\ &=\frac{(2n-3)(2n-5)\cdots 3}{(2n-2)(2n-4)\cdots 4}\int_{y=0}^{\pi/2}cos^2(y)dy\\ &=\frac{(2n-3)(2n-5)\cdots 3}{(2n-2)(2n-4)\cdots 4}\times \pi \end{aligned} \end{equation}\]输出功率为
\[\begin{equation} \begin{aligned} P&=cb\frac{(2n-3)(2n-5)\cdots 3}{(2n-2)(2n-4)\cdots 4}\times \pi=ERB*c \end{aligned} \end{equation}\]对于 \(n=4\)
\[\begin{equation} \begin{aligned} b=\frac{ERB}{\frac{(2n-3)(2n-5)\cdots 3}{(2n-2)(2n-4)\cdots 4}\times\pi}=ERB\frac{48}{15\pi} \approx 1.019ERB \end{aligned} \end{equation}\]